
Continuing on with the series, we will move on the support vector machines for programming assignment 6. If you had notice, I did not have a write-up for assignment 5 as most of the tasks just require plotting and interpretation of the learning curves. However, you can still find the code in my GitHub at https://github.com/Benlau93/Machine-Learning-by-Andrew-Ng-in-Python/tree/master/Bias_Vs_Variance.
There is two part in this assignment. First, we will implement Support Vector Machines (SVM) on several 2D data set to have an intuition of the algorithms and how it works. Next, we will use SVM on emails datasets to try and classify spam emails.
To load the dataset, loadmat from scipy.io is used to open the mat files
import numpy as np import pandas as pd import matplotlib.pyplot as plt from scipy.io import loadmatmat = loadmat("ex6data1.mat") X = mat["X"] y = mat["y"]
Plotting of the dataset
m,n = X.shape[0],X.shape[1]
pos,neg= (y==1).reshape(m,1), (y==0).reshape(m,1)
plt.scatter(X[pos[:,0],0],X[pos[:,0],1],c="r",marker="+",s=50)
plt.scatter(X[neg[:,0],0],X[neg[:,0],1],c="y",marker="o",s=50)

We start off with a simple dataset that has a clear linear boundary between the training examples.
As recommended in the lecture, we try not to code SVM from scratch but instead, make use of highly optimized library such as sklearn for this assignment. The official documentation can be found here.
from sklearn.svm import SVC
classifier = SVC(kernel="linear")
classifier.fit(X,np.ravel(y))

Since this is a linear classification problem, we will not be using any kernel for this task. This is equivalent to using the linear kernel in SVC (note that the default kernel setting for SVC is “ rbf”, which stands for Radial basis function). The
ravel() function here returns an array with size (m, ) which is required for SVC.plt.figure(figsize=(8,6)) plt.scatter(X[pos[:,0],0],X[pos[:,0],1],c="r",marker="+",s=50) plt.scatter(X[neg[:,0],0],X[neg[:,0],1],c="y",marker="o",s=50)# plotting the decision boundary X_1,X_2 = np.meshgrid(np.linspace(X[:,0].min(),X[:,1].max(),num=100),np.linspace(X[:,1].min(),X[:,1].max(),num=100)) plt.contour(X_1,X_2,classifier.predict(np.array([X_1.ravel(),X_2.ravel()]).T).reshape(X_1.shape),1,colors="b") plt.xlim(0,4.5) plt.ylim(1.5,5)

With the default setting of C = 1.0 (remember C = 1/λ), this is the decision boundary we obtained.
# Test C = 100
classifier2 = SVC(C=100,kernel="linear")
classifier2.fit(X,np.ravel(y))

plt.figure(figsize=(8,6)) plt.scatter(X[pos[:,0],0],X[pos[:,0],1],c="r",marker="+",s=50) plt.scatter(X[neg[:,0],0],X[neg[:,0],1],c="y",marker="o",s=50)# plotting the decision boundary X_3,X_4 = np.meshgrid(np.linspace(X[:,0].min(),X[:,1].max(),num=100),np.linspace(X[:,1].min(),X[:,1].max(),num=100)) plt.contour(X_3,X_4,classifier2.predict(np.array([X_3.ravel(),X_4.ravel()]).T).reshape(X_3.shape),1,colors="b") plt.xlim(0,4.5) plt.ylim(1.5,5)
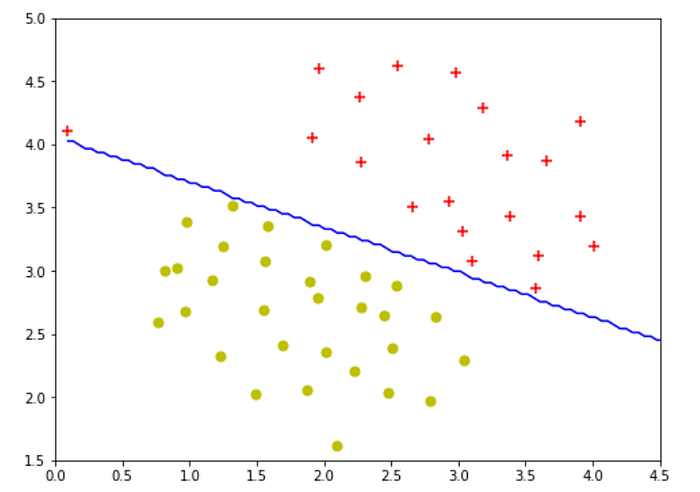
Changing C=100, gave a decision boundary that overfits the training examples.
Next, we will look at a dataset that could not be linearly separable. Here is where kernels come into play to provide us with the functionality of a non-linear classifier. For those having difficulties comprehending the concept of kernels, this article I found gave a pretty good intuition and some mathematics explanation about kernels. For this part of the assignment, we were required to complete the function
gaussianKernel to aid in the implementation of SVM with Gaussian kernels. I will be skipping this step as SVC contain its own gaussian kernels implementation in the form of Radial basis function (rbf). Here is the Wikipedia page with the equation for rbf, as you can see, it is identical to the Gaussian kernel function from the course.
Loading and plotting of example dataset 2
mat2 = loadmat("ex6data2.mat") X2 = mat2["X"] y2 = mat2["y"]m2,n2 = X2.shape[0],X2.shape[1] pos2,neg2= (y2==1).reshape(m2,1), (y2==0).reshape(m2,1) plt.figure(figsize=(8,6)) plt.scatter(X2[pos2[:,0],0],X2[pos2[:,0],1],c="r",marker="+") plt.scatter(X2[neg2[:,0],0],X2[neg2[:,0],1],c="y",marker="o") plt.xlim(0,1) plt.ylim(0.4,1)

To implement SVM with Gaussian kernels
classifier3 = SVC(kernel="rbf",gamma=30)
classifier3.fit(X2,y2.ravel())

In regards to the parameters of SVM with rbf kernel, it uses gamma instead of sigma. The documentation of the parameters can be found here. I found that gamma is similar to 1/σ but not exactly, I hope some domain expert can give me insights into the interpretation of this gamma term. As for this dataset, I found that gamma value of 30 shows the most resemblance to the optimized parameters in the assignment (sigma was 0.1 in the course).
plt.figure(figsize=(8,6)) plt.scatter(X2[pos2[:,0],0],X2[pos2[:,0],1],c="r",marker="+") plt.scatter(X2[neg2[:,0],0],X2[neg2[:,0],1],c="y",marker="o")# plotting the decision boundary X_5,X_6 = np.meshgrid(np.linspace(X2[:,0].min(),X2[:,1].max(),num=100),np.linspace(X2[:,1].min(),X2[:,1].max(),num=100)) plt.contour(X_5,X_6,classifier3.predict(np.array([X_5.ravel(),X_6.ravel()]).T).reshape(X_5.shape),1,colors="b") plt.xlim(0,1) plt.ylim(0.4,1)
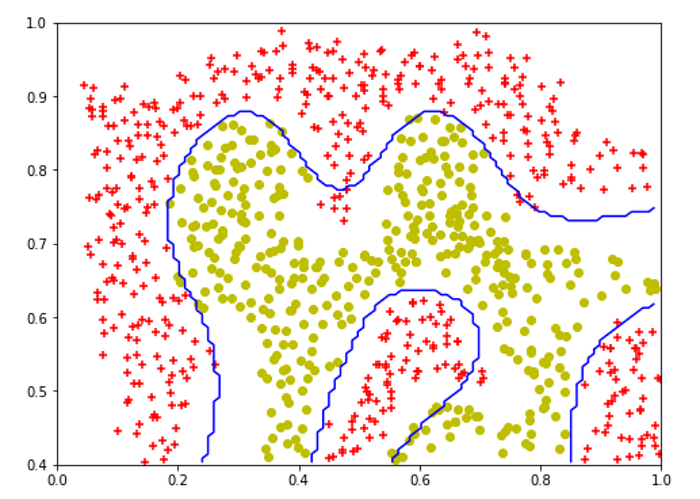
As for the last dataset in this part, we perform a simple hyperparameter tuning to determine the best C and gamma values to use.
Loading and plotting of examples dataset 3
mat3 = loadmat("ex6data3.mat") X3 = mat3["X"] y3 = mat3["y"] Xval = mat3["Xval"] yval = mat3["yval"]m3,n3 = X3.shape[0],X3.shape[1] pos3,neg3= (y3==1).reshape(m3,1), (y3==0).reshape(m3,1) plt.figure(figsize=(8,6)) plt.scatter(X3[pos3[:,0],0],X3[pos3[:,0],1],c="r",marker="+",s=50) plt.scatter(X3[neg3[:,0],0],X3[neg3[:,0],1],c="y",marker="o",s=50)

def dataset3Params(X, y, Xval, yval,vals):
"""
Returns your choice of C and sigma. You should complete this function to return the optimal C and
sigma based on a cross-validation set.
"""
acc = 0
best_c=0
best_gamma=0
for i in vals:
C= i
for j in vals:
gamma = 1/j
classifier = SVC(C=C,gamma=gamma)
classifier.fit(X,y)
prediction = classifier.predict(Xval)
score = classifier.score(Xval,yval)
if score>acc:
acc =score
best_c =C
best_gamma=gamma
return best_c, best_gamma
dataset3Params iterates through the list of vals given in the function and set C as vals and gamma as 1/vals. An SVC model is constructed using each combination of parameters and the accuracy of the validation set is computed. Based on the accuracy, the best model is chosen and the values for the respective C and gamma are returned.vals = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30]
C, gamma = dataset3Params(X3, y3.ravel(), Xval, yval.ravel(),vals)
classifier4 = SVC(C=C,gamma=gamma)
classifier4.fit(X3,y3.ravel())

plt.figure(figsize=(8,6)) plt.scatter(X3[pos3[:,0],0],X3[pos3[:,0],1],c="r",marker="+",s=50) plt.scatter(X3[neg3[:,0],0],X3[neg3[:,0],1],c="y",marker="o",s=50)# plotting the decision boundary X_7,X_8 = np.meshgrid(np.linspace(X3[:,0].min(),X3[:,1].max(),num=100),np.linspace(X3[:,1].min(),X3[:,1].max(),num=100)) plt.contour(X_7,X_8,classifier4.predict(np.array([X_7.ravel(),X_8.ravel()]).T).reshape(X_7.shape),1,colors="b") plt.xlim(-0.6,0.3) plt.ylim(-0.7,0.5)
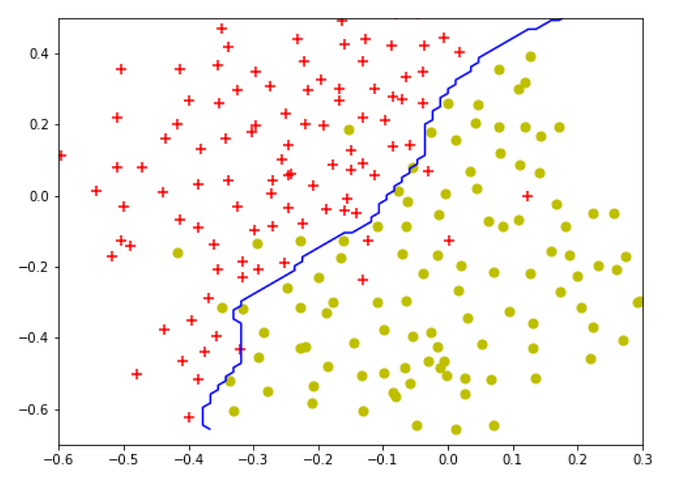
The optimal values are 0.3 for C and 100 for gamma, this results in similar decision boundary as the assginment.
Moving on to spam email classification. This problem is unique as it focuses more on data preprocessing than the actual modeling process. The emails need to process in a way that that could be used as input for the model. One way of doing so is to obtain the indices of all the words in an email based on a list of commonly used vocabulary.
Loading the data
import re from nltk.stem import PorterStemmerfile_contents = open("emailSample1.txt","r").read() vocabList = open("vocab.txt","r").read()

Vocabulary list and its respective indices were given, I had stored the list as a dictionary with the vocabs as keys and indices as values. You could probably do it another way but I want to make accessing the vocabs easier (eg. with
if keys in dict)vocabList=vocabList.split("\n")[:-1]vocabList_d={} for ea in vocabList: value,key = ea.split("\t")[:] vocabList_d[key] = value
As for preprocessing the emails, several steps were outlined for us in the assignment.
def processEmail(email_contents,vocabList_d): """ Preprocesses the body of an email and returns a list of indices of the words contained in the email. """ # Lower case email_contents = email_contents.lower() # Handle numbers email_contents = re.sub("[0-9]+","number",email_contents) # Handle URLS email_contents = re.sub("[http|https]://[^\s]*","httpaddr",email_contents) # Handle Email Addresses email_contents = re.sub("[^\s]+@[^\s]+","emailaddr",email_contents) # Handle $ sign email_contents = re.sub("[$]+","dollar",email_contents) # Strip all special characters specialChar = ["<","[","^",">","+","?","!","'",".",",",":"] for char in specialChar: email_contents = email_contents.replace(str(char),"") email_contents = email_contents.replace("\n"," ") # Stem the word ps = PorterStemmer() email_contents = [ps.stem(token) for token in email_contents.split(" ")] email_contents= " ".join(email_contents) # Process the email and return word_indices word_indices=[] for char in email_contents.split(): if len(char) >1 and char in vocabList_d: word_indices.append(int(vocabList_d[char])) return word_indicesword_indices= processEmail(file_contents,vocabList_d)
The use of regular expression comes in very handy here, this tutorial by python guru can help you get started on re. The other useful library here is nlkt where the
PorterStemmer() function helps with stemming the words. Another good tutorial here, this time by pythonprogramming.net.
After getting the indices of the words, we need to convert the indices into a features vector.
def emailFeatures(word_indices, vocabList_d): """ Takes in a word_indices vector and produces a feature vector from the word indices. """ n = len(vocabList_d) features = np.zeros((n,1)) for i in word_indices: features[i] =1 return featuresfeatures = emailFeatures(word_indices,vocabList_d) print("Length of feature vector: ",len(features)) print("Number of non-zero entries: ",np.sum(features))
The print statement will print:
Length of feature vector: 1899 and Number of non-zero entries: 43.0 . This is slightly different from the assignment as you’re was captured as “you” and “re” in the assignment while my code identified it as “your”, resulting in lesser non-zero entries.
To train the SVM will be as simple as passing the features as input. However, this is only one training example and we will need more training data to train a classifier.
spam_mat = loadmat("spamTrain.mat")
X_train =spam_mat["X"]
y_train = spam_mat["y"]
Training examples are given in
spamTrain.mat to train our classifier while test examples are in spamTest.mat to determine our model generalizability.C =0.1
spam_svc = SVC(C=0.1,kernel ="linear")
spam_svc.fit(X_train,y_train.ravel())
print("Training Accuracy:",(spam_svc.score(X_train,y_train.ravel()))*100,"%")
The print statement will print:
Training Accuracy: 99.825 %spam_mat_test = loadmat("spamTest.mat") X_test = spam_mat_test["Xtest"] y_test =spam_mat_test["ytest"]spam_svc.predict(X_test) print("Test Accuracy:",(spam_svc.score(X_test,y_test.ravel()))*100,"%")
The print statement will print:
Test Accuracy: 98.9 %
To better understand our model, we could look at the weights of each word and figure out the words that are most predictive of a spam email.
weights = spam_svc.coef_[0] weights_col = np.hstack((np.arange(1,1900).reshape(1899,1),weights.reshape(1899,1))) df = pd.DataFrame(weights_col)df.sort_values(by=[1],ascending = False,inplace=True)predictors = [] idx=[] for i in df[0][:15]: for keys, values in vocabList_d.items(): if str(int(i)) == values: predictors.append(keys) idx.append(int(values))print("Top predictors of spam:")for _ in range(15): print(predictors[_],"\t\t",round(df[1][idx[_]-1],6))

That's it for support vector machines! The jupyter notebook will be uploaded to my GitHub at (https://github.com/Benlau93/Machine-Learning-by-Andrew-Ng-in-Python).















thanks for this
ReplyDeleteBias, Machine Learning, Python, Support Vector Machines, SVM, Variance